Artykuły opublikowane w Mathematica Applicanda przy wsparciu Centrum
MATHEMATICA APPLICANDA, Vol. 41, No. 2 (2013), 171-184
The choice of a lawyer as a special case of self-insurance-cum-protection
Piotr Dudziński
[PDF]
Abstract. We consider decision about the choice of a lawyer as a particular case of self-insurance-cum-protection when the lawyer’s cost is repaid in case of victory. The problem was introduced by Sevi and Yafil (2005) in the context of self-protection, which requires assumption that the size of loss does not depend on effort (level of the expenditure on lawyer). In this paper we drop that assumption and our model includes possibility that both loss and probability of incuring a loss depend on effort. We compare effort in our case with the standard one and prove that repayment is good incentive to invest more in modified SICP. We also show that unlike the standard cases of SP and SICP, the level of effort is monotone in risk aversion. We prove that in our model DARA implies that lawyer’s service is a normal good, which is intuitive. We show that for certain type of increase in risk aversion, the reimbursement effect is stronger then the risk aversion effect. For other changes in risk aversion there is a probability threshold that if the probability of a loss is below that level, then risk-aversion effect prevails. For higher initial probabilities, reimbursement effect is stronger.
MATHEMATICA APPLICANDA, Vol. 43(1) 2015, p. 3–18
On the numerical detection of a bifurcation simplex in a curve
Jacek Gulgowski
[PDF]
Abstract. We present a numerical method which detects the presence and position of a bifurcation simplex, a regular 
-dimensional simplex, which may be considered as a ”fat bifurcation point”, in the curve of zeroes of the 
map 
. On the other hand, a bifurcation simplex appears in the neighbourhood of the bifurcation point, meaning that we have a method to approximately locate the bifurcation point as well. The method does not require any estimation of the derivative of the function 
and refers to the values of the map only through the vertices of certain triangulation. The bifurcation simplex is detected by a change
in the value of the Brouwer degree of the restriction of the map to the appropriate 
-simplex.
MATHEMATICA APPLICANDA, Vol. 43(2) 2015, p. 253–267
Efficient quadrature for fast oscillating integral of paraxial optics
Sergey Kshevetskii, Paweł Wojda
[PDF]
Abstract. The study concerns the determination of quadrature for the integral solution of the paraxial wave equation. The difficulty in computation of the integral is associated with the rapid change of the integrand phase. The developed quadrature takes into account the fast oscillating character of the integrand. The presented method is an alternative to the commonly used methods based on the use of the Fourier transform. The determination of the quadrature is discussed on the example of the integral arisen in the theory of propagation and focusing on hard X-rays waves. Due to the generality of the presented quadrature, it may also be applied to issues related to standard optics and acoustics.
MATHEMATICA APPLICANDA, Vol. 42(2) 2014, p. 179–192
The use of positioners in creating modular models of horns for mammals from the Bovidae family
Cezary Stępień, Małgorzata Prolejko
[PDF]
Abstract. This paper describes a method suitable for creating animated modular models of horns for mammals belonging to the Bovidae family. Our method uses time-dependent positioners—fragments of modules with their own coordinate systems. Positioners are used in two ways: for placing modules appropriately next to each other and for creating the lateral surfaces of modules. Thanks to this double usage of the positioners, a continuous surface is achieved, regardless of the complexity of the time-dependent parameters. Different connections between parameters of modules are considered, justified from the point of view of modeling horns. The method is illustrated with the example of creating a time-dependent model of a ram’s horn.
Weighted difference schemes for systems of quasilinear first order partial functional differential equations
Anna Szafrańska
[PDF]
Abstract. The paper deals with initial boundary value problems of the Dirichlet type for system of quasilinear functional differential equations. We investigate weighted difference methods for these problems. A complete convergence analysis of the considered difference methods is given. Nonlinear estimates of the Perron type with respect to functional variables for given functions are assumed. The proof of the stability of difference problems is based on a comparison technique. The results obtained here can be applied to differential integral problems and differential equations with deviated variables. Numerical examples are presented.
MATHEMATICA APPLICANDA, Vol. 41, No. 2 (2013), 185-198
Lower bound technique and its applications to function systems and stochastic partial differential equations
Tomasz Szarek
[PDF]
Abstract. We formulate some criteria on the existence of an invariant measure for Markov chains and Markov processes. We also show their utylities in the theory of function systems and stochastic differential equations.
MATHEMATICA APPLICANDA, Vol. 43(1) 2015, p. 19–35
Localization of genes
Piotr Szulc
[PDF]
Abstract. Development of genetics in recent years has led to a situation in which we are able to look at the DNA chains with high precision and collect vast amounts of information. In addition, it turned out that the relationships between genes and traits are more complex than previously thought. These two things caused the need for close collaboration between geneticists and mathematicians whose task is to develop special methods, coping with specific and difficult genetic problems. The article includes an overview of both classic and the latest approaches to the problem of localizing genes that indicate places in the DNA chain, which significantly influence the traits of interest to us. Because of not the best communication between mathematicians and geneticists, knowledge of methods other than the classic among the latter group is still small.
MATHEMATICA APPLICANDA, Vol. 43(1) 2015, p. 37–48
Application of 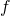RMSDchiral for the mathematical description of mutual position of stereoisomers
Rafał D. Urniaż
[PDF] [Supporting Information]
Abstract. The ability of biological systems to recognize and distinguish between compounds is crucial for living systems. A detailed study of this mechanism seems to be an important supplement to the analysis of possible interactions between compounds and the environment. This process could be characterized by a variety of descriptions of compounds’ structural and physico-chemical properties. The usual measure of variation in the positions of molecules in three dimensional space is the Root Mean Square Deviation (RMSD). Here, the traditional concept of RMSD was readjusted to fragment-level RMSD (RMSD). This assumes a different way of selecting atoms in molecules. The main aim is to appropriately group atoms into sets with respect to their chemical properties. In the case of enantiomers, atoms are selected according to the Cahn-Ingold-Prelog priority rule. The fRMSDchiral algorithm is applied to characterize the differences in modes of binding for some cases arising during our studies of molecular models of complexes formed between stereoisomers and their protein targets.
